Use Solver in Microsoft Excel unlocks a powerful tool for tackling complex problems in spreadsheets. This guide delves into the intricacies of this add-in, from its basic functionalities to advanced techniques, demonstrating how to leverage Solver for optimizing solutions in various scenarios. We’ll explore everything from setting up Solver problems to interpreting results and troubleshooting potential issues.

This comprehensive guide will equip you with the knowledge and skills to effectively use Solver, whether you’re a seasoned Excel user or just starting out. We’ll guide you through each step, providing practical examples and case studies to illustrate the real-world applications of this remarkable tool.

Table of Contents

Introduction to Solver in Excel

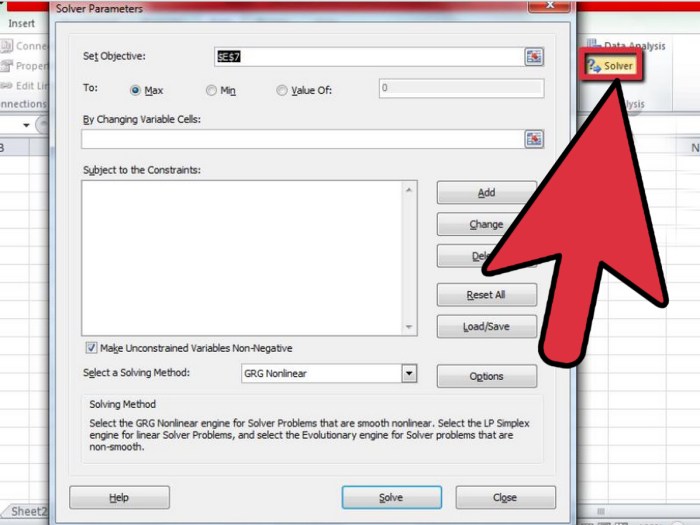
Solver is a powerful add-in in Microsoft Excel that helps you find optimal solutions to complex problems. It’s particularly useful for situations involving multiple variables and constraints, where a manual solution might be tedious or impossible. This tool is excellent for optimizing various scenarios, from resource allocation to financial modeling.The Solver tool automates the process of finding the best possible outcome by iteratively adjusting variables within predefined constraints.

This makes it a valuable asset for anyone working with mathematical models or looking to maximize or minimize specific values in spreadsheets.

Enabling the Solver Add-in

Before using Solver, you need to ensure it’s activated in your Excel installation. If it’s not already present in the ribbon, you need to load it. This is a simple process. Open Excel, and navigate to “File” > “Options” > “Add-ins.” In the “Manage” box, select “Excel Add-ins” and click “Go…”. Select the “Solver Add-in” from the list and click “OK.” Excel will then load the Solver add-in, and it will be available in the Data tab.

Solver Functions and Problem Types

Solver can tackle a wide range of optimization problems. Here’s a breakdown of common functions and problem types it addresses:

Solver Function	Problem Type	Brief Description
Maximize	Profit maximization, resource allocation	Finds the input values that result in the highest possible output value, given certain constraints.
Minimize	Cost reduction, material usage	Finds the input values that result in the lowest possible output value, subject to constraints.
Value of the objective cell	Target cell value	Sets a target value for a specific cell in the spreadsheet, and Solver adjusts other cells to achieve that target.
By Changing Variable Cells	Variable optimization	Identifies the values for specific cells that need to be adjusted to achieve the optimal outcome.
Subject to the Constraints	Limits on resources, production, or other factors	Defines the limitations or restrictions on the variables involved in the optimization process.

Common Use Cases

Solver is applicable in diverse fields. For instance, businesses can use it to optimize production schedules, maximize profits, or minimize costs. Financial analysts can use it to model investment strategies, find optimal portfolio allocations, or forecast future returns. In engineering, it can be used to design structures or systems to meet specific performance criteria.

Setting up Solver Problems

Solver in Excel is a powerful tool for finding optimal solutions to various problems. Once you’ve understood the basics of Solver’s functionality, the key lies in precisely defining the problem within Excel’s environment. This involves identifying the objective, the variables that can change, and any limitations or constraints. Proper setup ensures Solver delivers the intended results.Defining a Solver problem involves a meticulous process of identifying the objective function, the decision variables, and the constraints that shape the problem’s feasible space.

This setup directly translates into the specific mathematical formulation Solver uses to find the optimal solution. Accurately defining each element ensures Solver’s calculations produce a relevant and reliable result.

Defining the Objective Cell

The objective cell is the cell in your spreadsheet that represents the value you want to optimize. It’s the target of your Solver process, whether you want to maximize profit, minimize cost, or achieve a specific outcome. For example, if you’re aiming to maximize profit, the objective cell would contain the profit calculation formula.

Specifying Changing Cells

These are the cells whose values Solver will adjust to find the optimal solution. These are the variables that directly impact the objective cell’s value. You need to identify which cells are adjustable. For instance, in a production planning scenario, the changing cells might represent the quantity of different products to manufacture.

Establishing Constraints

Constraints are the limitations or restrictions placed on the changing cells. These ensure the solution is realistic and feasible within the problem’s context. These restrictions are often expressed as inequalities or equalities. For example, you might have constraints on the availability of resources or the capacity of production facilities. Common constraints include non-negativity, integer values, and limits on resource availability.

Types of Objective Functions

The objective function determines what Solver aims to optimize. You can choose to maximize or minimize a specific value. For example, you could maximize profit, minimize costs, or find the optimal production schedule. Here are common examples:

Maximization: Finding the highest possible value for the objective cell. An example would be maximizing profit in a sales forecasting model.
Minimization: Finding the lowest possible value for the objective cell. Minimizing costs for a transportation problem is a common use case.

Types of Constraints

Constraints define the boundaries within which Solver must search for a solution. Different types of constraints reflect various real-world limitations.

Non-negativity Constraints: These constraints ensure that the values of the changing cells are non-negative. For instance, you cannot produce a negative quantity of a product.
Integer Constraints: These constraints ensure that the values of the changing cells are integers. For example, if you are deciding how many machines to buy, the number must be a whole number.
Binary Constraints: These constraints ensure that the values of the changing cells are either 0 or 1. This is useful for situations like deciding whether to include or exclude a particular item in a product mix.
Resource Constraints: These constraints represent limitations on resources like materials, labor, or time. For example, a constraint might limit the total amount of raw materials available.

Illustrative Problem Types

The table below demonstrates different problem types, their objective functions, and examples of constraints.

Problem Type	Objective Function	Constraints
Profit Maximization (Sales Mix)	Maximize Total Profit	Resource Availability (materials, labor), Production Capacity, Non-negativity
Cost Minimization (Transportation)	Minimize Transportation Costs	Demand Requirements, Supply Limits, Non-negativity
Optimal Production Scheduling	Minimize Production Costs	Machine Capacity, Labor Availability, Material Availability, Non-negativity, Integer (number of units produced)

Solver Parameters and Options

The Solver add-in in Excel provides a powerful tool for finding optimal solutions to complex problems. Understanding its parameters and options is crucial for effectively leveraging this tool. Mastering these settings allows you to fine-tune the Solver’s approach, leading to more accurate and efficient results. From specifying the solving method to setting convergence criteria, these options offer significant control over the optimization process.Solver’s flexibility stems from its diverse parameters and options.

Choosing the appropriate method and adjusting convergence criteria are critical steps in ensuring accurate and reliable solutions. This control over constraints and tolerances allows users to tailor the Solver to their specific needs and problem complexities. This section will delve into the details of Solver’s parameters, enabling you to use it effectively.

Solving Methods

Solver offers various methods for finding optimal solutions. Choosing the correct method significantly impacts the Solver’s performance and the quality of the results. The selection depends on the nature of the optimization problem.

Simplex LP: This method is suitable for linear programming problems. It’s generally fast and efficient for such problems. Its effectiveness stems from its ability to explore the feasible region of the problem efficiently, locating the optimal solution quickly.
GRG Nonlinear: This method is designed for nonlinear problems. It employs a gradient-based approach, which can be computationally intensive for complex nonlinear functions. The gradient-based nature of GRG nonlinear methods allows for handling non-linear relationships within the optimization problem effectively.
Evolutionary: This method is often preferred for complex, non-linear problems that are difficult to solve using other methods. It utilizes a simulated evolution process to search for optimal solutions, making it useful for problems with many variables or complex relationships. The randomized nature of the method helps to explore a wider solution space, which is especially valuable for situations where other methods might struggle to locate optimal solutions.

Convergence Criteria

Convergence criteria define the conditions under which Solver stops searching for a solution. These criteria impact the accuracy and computational time of the optimization process. Setting appropriate criteria is crucial for achieving a balance between precision and efficiency.

Precision: The desired level of accuracy in the solution. A lower precision value will often lead to a faster solution but potentially lower accuracy. Higher precision may result in a more accurate solution but at the cost of increased computation time.
Iterations: The maximum number of iterations Solver will perform before stopping. Setting an appropriate iteration limit balances the search for the optimal solution with computational efficiency.
Tolerance: The acceptable level of error in the objective function or constraints. This setting influences the optimization process’s accuracy.

Constraints and Tolerances

Solver’s constraints and tolerances control the boundaries and limitations of the optimization problem. Adjusting these settings allows you to refine the solution space and ensure that the result aligns with specific requirements.

Constraint Types: Solver supports various constraint types, including less than or equal to, greater than or equal to, and equal to. Choosing the correct constraint type is essential to defining the problem’s boundaries.
Constraint Ranges: These define the numerical bounds within which the variables must fall. These are crucial in defining the feasible region.
Tolerance: This determines the degree of precision in the constraints. A smaller tolerance leads to a more precise solution but can increase the computational time.

Solver Parameter Table

Solver Parameter	Description	Default Value
Solving Method	Algorithm used to find the solution	GRG Nonlinear
Convergence Tolerance	Acceptable error in the objective function	0.0001
Iterations	Maximum number of iterations	100
Assume Non-Negative	Whether to constrain variables to be non-negative	Checked
Scaling	Whether to scale the variables	Checked

Solving and Interpreting Results

Once you’ve set up your Solver problem correctly, the next crucial step is executing the solution and interpreting the results. This involves understanding not just the optimal solution but also the underlying assumptions and potential limitations. A comprehensive understanding of the Solver results is essential for making informed decisions based on the analysis.

Running the Solver

After configuring the Solver parameters, initiating the solution process is straightforward. Click the “Solve” button. The Solver will then attempt to find the optimal solution that satisfies the constraints you’ve defined. The process may take a varying amount of time depending on the complexity of the problem and the computational resources available. During this time, it’s important to monitor the Solver’s progress to avoid interruptions or errors.

Interpreting Solver Results

The Solver’s output includes the optimal values for the decision variables, as well as the objective function’s optimal value. This output directly reflects the solution to your defined problem. Crucially, it’s essential to understand the context of these values within the broader problem setup. Furthermore, Solver provides valuable insights into the sensitivity of the solution to changes in parameters.

Analyzing the Solution

Beyond the optimal values, a thorough analysis of the solution should include examining the constraints. Did any constraints become binding? Understanding which constraints were active in achieving the optimal solution is crucial for comprehending the trade-offs involved. A review of the sensitivity report provides insights into how changes in input parameters affect the optimal solution.

Ever feel stuck with a spreadsheet problem in Excel? Using Solver can be a game-changer, finding optimal solutions to complex calculations. It’s like having a super-powered calculator for your data, and it’s surprisingly intuitive once you get the hang of it. Speaking of finding solutions, it’s awesome to see Tame Impala headline Desert Daze with a special set celebrating the 10th anniversary of their album Lonerism! tame impala to headline desert daze with lonerism 10th anniversary set.

Learning Solver will definitely make your Excel work a whole lot smoother, and I’m already planning my next spreadsheet adventure.

Solution Statuses

Solver provides different statuses to indicate the outcome of the solution process. Understanding these statuses is vital for interpreting the results.

Optimal: This signifies that the Solver has found a solution that optimizes the objective function while satisfying all constraints. This is the ideal scenario and usually represents the most efficient outcome.
Unbounded: This indicates that the objective function can be improved indefinitely without violating any constraints. This usually arises from a problem with the model’s structure or a flaw in the objective function’s definition.
Infeasible: This means no solution exists that satisfies all the constraints simultaneously. This necessitates revisiting the problem formulation or constraints to identify any conflicting or impossible requirements.
No Feasible Solution: This suggests that the solver cannot find a solution that satisfies all the constraints. This requires checking for any mistakes in the model’s formulation, including data input accuracy.

Comparison of Solution Statuses

The table below summarizes the different solution statuses and their interpretations.

Solution Status	Interpretation
Optimal	A solution satisfying all constraints and optimizing the objective function has been found.
Unbounded	The objective function can be improved indefinitely without violating any constraints.
Infeasible	No solution exists that satisfies all constraints simultaneously.
No Feasible Solution	The solver cannot find a solution that satisfies all constraints.

Advanced Solver Techniques: Use Solver In Microsoft Excel

Solver, while a powerful tool for basic optimization, truly shines when tackling complex scenarios. This exploration dives deeper into advanced techniques, allowing you to leverage Solver’s capabilities to solve multifaceted problems beyond simple linear relationships. From handling multiple constraints to navigating non-linear landscapes and integer requirements, we’ll equip you with the knowledge to unlock Solver’s full potential.

Multiple Constraints

Adding multiple constraints to a Solver problem is crucial for modeling real-world situations with their diverse limitations. These constraints can be of various types, such as budget restrictions, resource availability, or production capacity. Solver handles these by optimizing the objective function while adhering to all defined limitations. A key consideration is how these constraints interact and whether they lead to feasible solutions.

Ever wished you could effortlessly find the optimal solution in your Excel spreadsheets? Using Solver is a game-changer for complex calculations. Just like Amerie’s exciting announcement of her first new album in nine years, amerie announces first new album in 9 years , finding the right figures in spreadsheets can be just as rewarding. Solver helps you optimize formulas and achieve desired outcomes, making your data analysis so much smoother.

Complex systems might have conflicting constraints, requiring careful formulation to find an optimal balance.

Non-Linear Optimization

Many real-world scenarios involve non-linear relationships between variables. For instance, the relationship between production output and costs might not be linear. Solver can tackle these non-linear challenges, albeit with potential limitations. The iterative nature of the Solver algorithm can sometimes struggle with complex non-linear functions.

Integer Programming

Integer programming problems require solutions that involve integer values, not just decimals. This is important in situations where you need whole numbers for quantities, like the number of units produced or employees hired. Using integer constraints often leads to a more practical and realistic outcome. Common examples include scheduling problems, where assigning employees to shifts often requires whole numbers.

Multiple Objectives

Solver can be extended to address problems with multiple objectives, not just one. Consider a manufacturing scenario where minimizing costs and maximizing output are both critical. Solver allows you to define these multiple objectives, with weights assigned to each objective to prioritize certain outcomes.

Limitations and Alternatives

Solver, while powerful, has limitations. Complex non-linear problems or those with numerous variables might prove challenging to solve or require significant computational time. For such scenarios, specialized optimization software or other analytical techniques might be more suitable. For example, if the problem involves intricate non-linear equations, advanced numerical methods might provide more accurate and efficient solutions.

Comparison of Advanced Techniques

Technique	Description	Application	Limitations
Multiple Constraints	Solver handles multiple limitations in a problem.	Resource allocation, budget constraints, production capacity	Potential for conflicting constraints.
Non-Linear Optimization	Addresses problems with non-linear relationships.	Cost-output relationships, supply chain optimization	Computational demands, algorithm limitations.
Integer Programming	Ensures integer values in solutions.	Scheduling, resource allocation, product configuration	Computational intensity increases with complexity.
Multiple Objectives	Simultaneously optimizes multiple objectives.	Balancing cost and output, minimizing risk and maximizing return	Defining appropriate weights for objectives.

Practical Examples and Case Studies

Solver’s power extends beyond theoretical demonstrations. Its practical applications in real-world business scenarios are numerous and impactful. From optimizing production schedules to fine-tuning resource allocation, Solver can provide valuable insights and drive significant improvements in efficiency and profitability. This section delves into several practical examples showcasing Solver’s effectiveness in diverse industries.Solver’s ability to model complex business problems allows decision-makers to explore various scenarios and identify optimal solutions.

By defining objective functions and constraints, Solver systematically finds the best possible outcome within the specified limitations. The examples below highlight the versatility of Solver, demonstrating how it can be applied in different industries and for diverse business needs.

Budgeting Optimization

Effective budgeting requires careful consideration of various factors. Solver can assist in optimizing budgets by considering constraints like available funds and required expenditures. This optimization can be crucial for achieving desired financial outcomes while adhering to pre-defined limits.

Example: A company needs to allocate a budget of $100,000 across three departments: Marketing, Sales, and Research & Development (R&D). The company has specific targets for each department, and the budget allocation needs to consider these targets while minimizing costs.
Problem Description: Allocate the budget across departments to maximize overall company performance while staying within the budget limit.
Solver Setup: Objective function: Maximize overall performance (e.g., a weighted sum of departmental targets). Constraints: Total budget must not exceed $100,000; budget allocation for each department must be non-negative.
Results: Solver determines the optimal budget allocation for each department, ensuring the total budget constraint is met and maximizing the weighted performance score.

Resource Allocation

Optimizing resource allocation is essential for maximizing productivity and minimizing costs. Solver can be employed to determine the optimal allocation of resources, such as labor, materials, or equipment, to specific tasks. This ensures that resources are utilized effectively and efficiently.

Example: A manufacturing company needs to assign 10 workers to 5 different production lines. Each worker has varying skills, and each production line has different task demands. The goal is to maximize production output.
Problem Description: Assign workers to production lines to maximize overall output, considering worker skills and production line demands.
Solver Setup: Objective function: Maximize total production output. Constraints: Each worker can only be assigned to one production line; each production line requires a minimum number of workers; worker skills must match production line requirements.
Results: Solver identifies the optimal worker assignments to each production line, maximizing production output while considering the constraints.

Inventory Management

Effective inventory management is crucial for maintaining profitability and avoiding stockouts or overstocking. Solver can be applied to optimize inventory levels, considering factors like demand forecasting, lead times, and storage costs.

Ever wondered how to optimize things in Excel? Using Solver is a fantastic tool for finding the best solutions to complex problems. It’s incredibly helpful for figuring out tricky scenarios, and can be a real game-changer. For instance, if you’re looking for the perfect balance of glass candy and Halloween treats for your next listenwatch glass candy halloween extravaganza, Solver can help you nail the perfect mix! listenwatch glass candy halloween Ultimately, Solver in Excel is a powerful tool that can solve many different kinds of problems, not just sweet ones!

Example: A retailer needs to determine the optimal inventory levels for a specific product, considering historical sales data, predicted demand, and storage costs.
Problem Description: Determine the optimal inventory levels to meet demand while minimizing storage costs and the risk of stockouts.
Solver Setup: Objective function: Minimize total inventory costs (holding costs + shortage costs). Constraints: Demand must be met; inventory levels must be non-negative.
Results: Solver provides the optimal inventory level, balancing demand fulfillment with cost minimization.

Troubleshooting Solver Issues

Solver, a powerful tool in Excel, can sometimes encounter roadblocks. Understanding common issues and their resolutions is crucial for effective optimization. This section delves into diagnosing and resolving these problems, from infeasible solutions to solver non-convergence. By familiarizing yourself with these troubleshooting steps, you’ll gain a significant advantage in effectively utilizing Solver’s capabilities.

Common Solver Errors

Identifying and addressing errors is key to successful Solver implementation. Common errors include Solver not finding a solution, encountering infeasible or unbounded solutions, and problems with constraints. Each of these scenarios has specific troubleshooting procedures.

Solver Cannot Find a Solution: Solver might fail to find a solution due to various reasons. These could range from incorrect model setup to inadequate search options. Thoroughly checking your constraints and objective function for errors is essential. Re-evaluating the model’s assumptions and potential inconsistencies can help identify the root cause. Sometimes, simply restarting Excel and running Solver again can resolve the issue.
Infeasible Solutions: An infeasible solution indicates that no combination of values for the decision variables can satisfy all the constraints simultaneously. This typically stems from conflicting or overly restrictive constraints. Carefully examine each constraint to identify any contradictions. Relaxing or modifying constraints, potentially adjusting their values, is a crucial troubleshooting step. Alternatively, checking for redundant or unnecessary constraints might reveal the issue.
Unbounded Problems: An unbounded problem signifies that the objective function can improve indefinitely without violating any constraints. This often results from missing or inappropriate constraints that limit the decision variables’ range. Adding constraints that bound the variables’ values can often solve this problem. Reconsidering the model’s structure and the potential for the solution to be unbounded is important. For example, a lack of constraints on a variable might allow it to grow indefinitely.
Solver Not Converging: Solver’s failure to converge to a solution can stem from various factors, including poor initial guesses, an ill-posed problem, or issues with the optimization algorithm. Checking for appropriate scaling of variables is a significant step. Solver’s convergence relies on iterative methods. Consider using different algorithms if the default one fails to converge. Restating the model to simplify its structure and address potential conflicts is another important step.

Troubleshooting Steps, Use Solver in Microsoft Excel

A structured approach to troubleshooting Solver issues can save valuable time. Follow these steps for effective diagnosis and resolution:

Verify Model Setup: Carefully review the objective function, decision variables, and constraints. Ensure all values and formulas are correctly entered. Look for typos or errors in the formulas and constraints. Double-checking the input data and model setup is a crucial first step.
Examine Constraints: Thoroughly inspect each constraint. Are there any inconsistencies or contradictions? Ensure the constraints are properly defined to reflect the real-world limitations. Consider modifying or relaxing constraints to see if this resolves the problem.
Check Solver Options: Adjust Solver parameters such as the maximum iterations or tolerance. Experiment with different algorithms if the default algorithm isn’t working. These settings can significantly impact Solver’s performance and ability to find a solution.
Try Different Initial Values: Solver often starts with default values. Experiment with different initial values for decision variables to see if this affects the outcome. If the problem is highly sensitive to initial values, consider employing techniques to improve the initial guess.
Simplify the Model: In some cases, simplifying the model might reveal the source of the issue. Removing non-essential constraints or variables can make the problem easier to solve. Simplify the model to identify if the issue persists in a more manageable representation.

Common Solver Errors and Troubleshooting

This table provides a concise overview of common Solver errors and their troubleshooting steps.

Error	Troubleshooting Steps
Solver could not find a feasible solution.	Verify constraints, check for inconsistencies, adjust constraint values, and try different initial guesses.
Solver could not find a solution.	Re-examine model setup, check for errors in formulas, and adjust Solver parameters (tolerance, maximum iterations).
Solver could not converge to a solution.	Ensure proper scaling of variables, try a different optimization algorithm, and potentially simplify the model.
Unbounded solution.	Check for missing or inappropriate constraints that limit the decision variables’ range. Add constraints to bound the variables.

Final Conclusion

In conclusion, mastering Solver in Excel empowers you to solve optimization problems efficiently and effectively. This guide has explored the fundamentals and advanced techniques, providing a solid foundation for utilizing Solver in diverse scenarios. From simple budgeting to complex resource allocation, Solver provides a powerful solution-finding engine. Remember to practice these techniques to truly grasp their power. By understanding Solver’s functionalities and limitations, you’ll gain valuable skills that enhance your problem-solving abilities in Excel and beyond.