Create an S Curve Pattern in Microsoft Excel sets the stage for mastering data analysis techniques. This comprehensive guide dives deep into creating, interpreting, and visualizing S-curves using Microsoft Excel. We’ll explore the intricacies of data preparation, the selection of appropriate modeling methods, and the implementation of S-curve fitting in Excel. From understanding the core concepts to practical applications, this journey will equip you with the knowledge and tools to confidently tackle S-curve analysis in various fields.
The guide will cover the different types of S-curves, including logistic and Gompertz models, and discuss their respective advantages and disadvantages. It will also delve into the crucial aspects of data preparation, emphasizing the importance of data cleaning and validation. Visualizing these curves in Excel, creating compelling charts and graphs, and understanding the elements for effective visualization will be central themes.
Introduction to S-Curve Patterns: Create An S Curve Pattern In Microsoft Excel
An S-curve pattern, a common graphical representation in various fields, depicts a gradual increase in a quantity over time, initially slow, then accelerating, and finally leveling off. It’s a powerful tool for understanding trends and anticipating future performance. The shape mirrors the natural growth cycles often observed in technological advancements, market penetration, and project timelines.This pattern is characterized by its distinct phases, reflecting different stages of development or implementation.
Understanding the characteristics of each phase allows for better planning, resource allocation, and risk management. S-curve analysis provides valuable insights into the potential for future growth and the associated challenges. It’s widely applicable across numerous industries, from project management to sales forecasting.
Typical Characteristics of an S-Curve
The S-curve’s characteristic shape is derived from the interplay of several factors. It starts with a slow, gradual increase, often representing the initial phase of development or implementation where resources are being allocated and infrastructure built. This phase is followed by a period of accelerating growth, where the momentum increases and significant progress is made. Finally, the growth rate slows and plateaus, reaching a maximum capacity or saturation point.
The shape itself resembles the letter ‘S’ on a graph.
Practical Applications of S-Curve Analysis
S-curve analysis is a valuable tool in diverse fields. In project management, it helps visualize project progress, anticipate potential delays, and adjust resource allocation as needed. By plotting the project’s actual progress against the predicted S-curve, deviations can be identified early on, enabling proactive adjustments. In sales forecasting, it allows businesses to predict future sales revenue based on historical data and market trends.
The predicted S-curve helps in setting realistic targets and anticipating periods of rapid growth or slower progress. In technology adoption, it can predict how quickly a new product or service will gain market share.
Stages of an S-Curve and Potential Issues
Understanding the different stages of an S-curve and the associated potential issues is crucial for effective management and planning.
| Stage of the S-curve | Typical Characteristics | Potential Issues |
|---|---|---|
| Initial Stage (Slow Growth) | Low output, investment in infrastructure, learning curve, and development. | Insufficient resources, delays, low motivation, and lack of clear direction. |
| Accelerating Stage (Rapid Growth) | Increased output, high efficiency, and significant progress. | Demand outpacing supply, insufficient skilled workforce, and potential quality issues. |
| Maturing Stage (Decelerating Growth) | Output growth slows, approaching saturation, and efficiency stabilizes. | Stagnation, decreased motivation, difficulty in sustaining growth, and need for innovation. |
| Plateau Stage (Saturation) | Output stabilizes at a maximum capacity. | Maintaining market share, adapting to changing market conditions, and identifying new growth opportunities. |
Data Preparation for S-Curve Creation
Preparing your data meticulously is crucial for accurately fitting an S-curve. A poorly prepared dataset can lead to an inaccurate model, misinterpretations, and ultimately, flawed predictions. This section details the essential steps for data cleaning, validation, and handling missing data and outliers to ensure your S-curve model is reliable and robust.
Creating an S curve pattern in Excel can be a useful tool for visualizing growth, and I’ve been experimenting with it lately. It’s fascinating how these patterns emerge from data, and it’s a great way to represent trends. For example, if you were analyzing a music festival like the lollapalooza report saturday joshua klein , you might use an S curve to chart the attendance throughout the day.
Ultimately, understanding how to craft these curves in Excel allows for a deeper insight into the data itself.
Data Cleaning and Validation
Thorough data cleaning and validation are essential steps in the process. Errors in the data can significantly skew the results of the S-curve fitting process. Inconsistencies, inaccuracies, or irrelevant data points can distort the shape of the curve and produce unreliable predictions. Identifying and addressing these issues upfront ensures the model’s accuracy and reliability.
- Data Inspection: Carefully examine the data for any inconsistencies, errors, or outliers. This initial review helps identify patterns and potential problems. Look for discrepancies in units, formatting, or illogical values that might need correction.
- Data Validation Rules: Establish clear rules for validating the data. This involves defining acceptable ranges, formats, and types of values for each data point. For example, if the data represents sales figures, ensure values are positive numbers. Defining these rules helps catch errors and inconsistencies early in the process.
- Data Transformation: If needed, transform the data to a suitable format for S-curve fitting. This might involve converting units, scaling values, or applying mathematical functions to align with the expected model input.
Handling Missing Data Points
Missing data points are a common issue in datasets. These gaps can significantly affect the accuracy of the S-curve model. Appropriate strategies for handling missing values are necessary to ensure the model’s reliability.
- Identifying Missing Data: First, identify which data points are missing. Use Excel’s built-in tools or custom formulas to locate these gaps in the dataset. This will allow you to implement a suitable strategy.
- Imputation Techniques: Several imputation techniques can be used to fill in missing data points. For example, you can use the mean, median, or mode of the existing data to estimate the missing values. More sophisticated methods, like regression imputation, can also be considered for more complex datasets.
- Removal of Data Points: In certain cases, removing the data points with missing values might be the best approach. This strategy is usually only recommended if the proportion of missing data is relatively small and doesn’t significantly impact the overall dataset.
Handling Outliers
Outliers are extreme values that deviate significantly from the majority of the data points. These outliers can skew the results of the S-curve fitting process. It’s crucial to identify and address outliers appropriately.
- Identifying Outliers: Use visual methods like scatter plots or box plots to identify potential outliers. Statistical methods like calculating the interquartile range (IQR) can also help pinpoint extreme values.
- Investigating Outliers: Once identified, investigate the reasons behind the outliers. They might be genuine data points or errors in data entry. Understanding the source of the outliers helps determine the best course of action.
- Handling Outliers: Strategies for handling outliers include removing them, transforming the data to reduce their impact, or using robust statistical methods that are less sensitive to extreme values.
Data Preparation Steps
| Step | Description | Tools/Techniques |
|---|---|---|
| 1 | Inspect the data for inconsistencies, errors, and outliers. | Visual inspection, data profiling tools |
| 2 | Establish data validation rules. | Excel formulas, data validation features |
| 3 | Transform the data if necessary. | Excel formulas, data transformation functions |
| 4 | Identify and handle missing data points. | Excel formulas, imputation techniques (mean, median, mode, regression) |
| 5 | Identify and handle outliers. | Visualizations (scatter plots, box plots), statistical methods (IQR), data transformation |
Selecting Suitable Methods for S-Curve Modeling
Crafting an S-curve in Excel involves choosing the right modeling technique. The best approach depends on the nature of your data and the desired level of accuracy. This section delves into various methods, highlighting their strengths and weaknesses to aid your decision-making process.
Methods for S-Curve Creation
Different techniques can be employed to construct S-curves in Excel. These range from simple trendline fitting to more complex custom functions or specialized add-ins. Understanding the characteristics of each method is crucial for selecting the most appropriate one for your specific data.
Trendlines
Trendlines are a straightforward and readily available tool within Excel. They offer a visual representation of data trends, which can be helpful for approximating an S-curve. However, their inherent limitations in capturing the nuanced shape of an S-curve should be considered.
- Advantages: Ease of use, readily available within Excel, provides a visual representation of data trends.
- Disadvantages: May not accurately capture the inflection points and asymptotic behavior characteristic of S-curves, especially for complex data sets. Requires careful selection of the appropriate trendline type.
- Suitability: Suitable for relatively simple data sets where a general trend approximation is sufficient. Not ideal for highly complex or precise S-curve modeling.
Custom Functions
Custom functions allow for greater flexibility in defining the shape of the S-curve. These functions can be tailored to specific data characteristics, potentially leading to a more accurate representation. Developing these functions, however, requires a deeper understanding of mathematical modeling and programming in Excel.
- Advantages: High degree of customization, potentially greater accuracy, allows for incorporation of specific data characteristics.
- Disadvantages: Requires programming knowledge and careful function design. May be computationally intensive, particularly for complex functions. Potential for errors in the function definition leading to inaccurate results.
- Suitability: Suitable for complex data sets where trendlines are insufficient. Best employed when a strong understanding of the underlying mathematical principles driving the S-curve is available.
Specialized Add-ins
Specialized Excel add-ins offer pre-built tools for creating and analyzing S-curves. These often include sophisticated algorithms and statistical methods, potentially leading to higher accuracy and ease of use. The availability and suitability of these add-ins depend on the specific software package used.
- Advantages: Often include advanced algorithms and statistical methods, potentially increasing accuracy, streamlined workflow, and user-friendly interfaces.
- Disadvantages: Cost or licensing requirements, potential incompatibility with other software, may require additional learning curves for the specific add-in. Not all add-ins may perfectly fit all datasets.
- Suitability: Suitable for cases where high accuracy and efficiency are paramount, or when a large number of S-curves need to be generated. Ideal for users with advanced technical skills who require specialized features.
Comparison Table
| Method | Advantages | Disadvantages | Suitability |
|---|---|---|---|
| Trendlines | Ease of use, visual representation | Limited accuracy, may not capture inflection points | Simple data sets, general trend approximation |
| Custom Functions | High customization, potentially greater accuracy | Requires programming knowledge, computational intensity | Complex data sets, strong understanding of S-curve |
| Specialized Add-ins | Advanced algorithms, streamlined workflow | Cost/licensing, potential incompatibility, learning curve | High accuracy required, numerous S-curves needed |
Implementing S-Curve Modeling in Excel
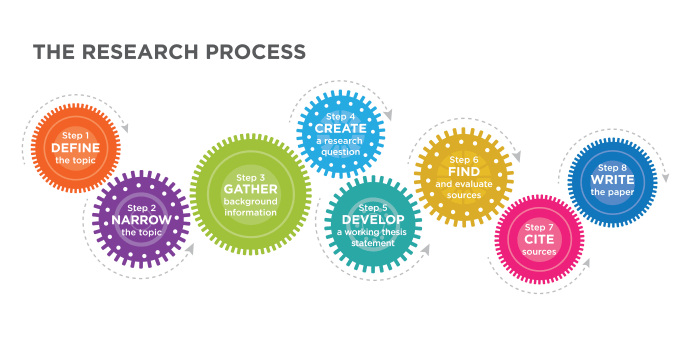
S-curve modeling is a powerful technique for analyzing and predicting growth patterns. Understanding how to implement these models in Excel allows for the visualization and interpretation of data in a meaningful way. This section dives into the practical application of S-curve fitting within Microsoft Excel, providing detailed steps and examples.Excel’s built-in tools provide a straightforward approach to fitting S-curves to your data.
These tools, combined with a solid understanding of the underlying models, empower you to extract valuable insights from your data.
Using Excel’s Trendline Feature
Excel’s trendline feature simplifies the process of creating S-curve models. This feature allows for the visual representation of the data’s trend and the fitting of various types of curves, including S-curves. Different types of S-curves are better suited to different types of data.
To create a trendline in Excel, select the data points on the chart, right-click, and choose “Add Trendline.” From the “Trendline Options” dialog box, select the desired S-curve type. This dialog box usually offers various options like exponential, logarithmic, polynomial, moving average, and more.
Polynomial Fitting for S-Curves
Polynomial fitting is a versatile method for modeling S-curves. It involves using a polynomial function to approximate the relationship between variables in the dataset. This method can effectively capture various growth patterns, though it may require careful consideration of the degree of the polynomial to avoid overfitting.A higher-degree polynomial can fit the data more closely, but may not accurately reflect the underlying trend.
Figuring out how to create an S curve pattern in Excel can be tricky, but it’s a useful skill for visualizing trends. While I was researching different methods, I stumbled upon some exciting news about turnstile announce the never enough tour here. Getting that S curve just right in your spreadsheet is rewarding, especially when you’re analyzing data and trying to understand its direction.
The best degree is determined by evaluating the model’s performance.
Different Types of S-Curves
Various mathematical models describe S-curve patterns. Each model has unique characteristics and is suitable for specific data scenarios.
- Logistic Curve: This model is characterized by an initial slow growth rate, followed by an accelerated growth phase and finally, a deceleration as it approaches saturation. It is commonly used to model population growth or market penetration.
- Gompertz Curve: This model also depicts an S-shaped growth pattern. However, it’s characterized by a more pronounced initial lag phase and a faster deceleration compared to the logistic curve. It is often used to model biological growth processes.
Formulas Behind S-Curve Models
The mathematical equations underpinning S-curve models determine their behavior. These formulas dictate the shape and characteristics of the curve.
- Logistic Function: y = L / (1 + e (-k(x – x0)) ), where L is the maximum value, k is the growth rate, and x 0 is the x-value at the midpoint of the curve.
- Gompertz Function: y = L
– e (-e(-k(x – x0)) ) , where L is the maximum value, k is the growth rate, and x 0 is the x-value at the midpoint of the curve.
Step-by-Step Procedure for Fitting an S-Curve (Example: Logistic Curve)
This example Artikels fitting a logistic curve using Excel’s trendline feature.
- Data Preparation: Ensure your data is organized with x-values (independent variable) in one column and y-values (dependent variable) in another.
- Create a Scatter Plot: In Excel, create a scatter plot with your data points.
- Add Trendline: Right-click on the data points, select “Add Trendline,” and choose “More Options.” In the “Trendline Options” dialog box, select “Logistic” from the “Trendline type” dropdown menu.
- Display Equation: Ensure the “Display Equation on chart” option is checked.
- Display R-squared: Check the “Display R-squared value on chart” option for assessing goodness of fit.
- Analyze Results: Interpret the equation and R-squared value to understand the fitted curve and its accuracy.
Interpreting and Analyzing the S-Curve
The S-curve, a graphical representation of cumulative progress over time, reveals valuable insights into project performance and forecasting. Understanding its parameters and inflection points is crucial for effective project management and strategic decision-making. This analysis extends beyond simple visual interpretation to incorporate statistical methods for assessing the accuracy of the model and its predictions.Interpreting the S-curve involves examining the shape, identifying key points, and analyzing the underlying data to derive meaningful conclusions.
The parameters of the model, combined with the visual representation, offer a powerful tool for forecasting and trend identification. The analysis extends to the identification of error sources and the evaluation of the model’s accuracy to ensure reliable predictions.
Interpreting Model Parameters
Model parameters are essential for understanding the S-curve’s characteristics. These parameters dictate the curve’s shape, growth rate, and eventual saturation point. Different mathematical models generate various parameters. For example, the logistic function often yields parameters such as the growth rate, initial value, and carrying capacity. Careful analysis of these parameters provides insight into the factors driving the observed pattern.
Forecasting Future Values
The S-curve can be used to forecast future values or trends by extrapolating the observed pattern. By fitting a suitable model to historical data, the curve can project future performance. For instance, in software development, an S-curve representing cumulative features implemented over time can be used to forecast the completion date of a project based on the model’s predictions.
However, it’s important to acknowledge that forecasting relies on the model’s accuracy and the validity of its assumptions.
Identifying Inflection Points
Inflection points, where the curve changes its concavity, are significant turning points on the S-curve. These points often indicate shifts in the underlying process or project dynamics. For instance, a rapid increase in the S-curve’s slope might signal the introduction of new resources or a change in strategy. Recognizing these shifts is crucial for adjusting project plans and strategies accordingly.
Importance of Error Analysis
Error analysis is vital in evaluating the accuracy of the S-curve model. Calculating the difference between the predicted values and the actual data points reveals potential sources of error. This analysis can help identify model shortcomings or data anomalies. Statistical measures like the coefficient of determination (R-squared) and root mean squared error (RMSE) are used to quantify the model’s fit and identify potential areas for improvement.
Figuring out how to create an S curve pattern in Excel can be tricky, but it’s definitely doable. While exploring the visual intricacies of this pattern, I stumbled upon some amazing photos of Erykah Badu and Janelle Monáe, showcasing their unique styles photos erykah badu janelle monae. Getting back to the task at hand, the key to creating a smooth S curve in Excel lies in understanding the data points and using the right charting tools.
It’s a satisfying process, and hopefully these tips help you tackle your own Excel S curves.
Assessing Goodness of Fit
Assessing the goodness of fit of the S-curve to the data is crucial for determining its reliability. Various statistical measures, like R-squared, are used to quantify the proportion of variance in the data explained by the model. A high R-squared value indicates a good fit, while a low value suggests the model may not accurately represent the underlying trend.
Visual Representation Elements
A clear visual representation of an S-curve should include several key elements. These include properly labeled axes (time on the x-axis and cumulative value on the y-axis), a clear plot of the data points, and the fitted S-curve overlaid on the data. The visual representation should also include any relevant annotations, such as inflection points, trend lines, and error bars.
A well-structured visualization allows for quick comprehension of the project’s progress and future projections. Color-coding data points based on categories (e.g., different phases of a project) can further enhance the visualization.
Case Studies and Practical Examples
S-curves aren’t just theoretical constructs; they’re powerful tools for understanding and predicting growth patterns in various industries. This section dives into real-world applications, showcasing how S-curves can provide actionable insights. We’ll explore the data sources used, analyze results, and demonstrate a practical step-by-step approach for implementing this method on your own data.Understanding how S-curves manifest in diverse industries allows for more informed decision-making.
Analyzing successful implementations reveals patterns and best practices, offering a roadmap for your own S-curve analyses.
Real-World S-Curve Applications, Create an S Curve Pattern in Microsoft Excel
Various sectors leverage S-curves to track progress and anticipate future trends. Examples include market penetration of new technologies, product adoption rates, and the scaling of production processes. A crucial aspect is recognizing that the specific shape and inflection points of an S-curve vary greatly depending on the industry and the factors influencing it.
- Technology Adoption: The adoption of smartphones, initially slow, rapidly increased after overcoming initial hurdles like price and infrastructure limitations. Data sources for this analysis would include market share reports from companies like IDC and Gartner, alongside sales data from manufacturers and carriers. Analysis reveals a clear S-curve pattern, with rapid growth occurring after a period of slower initial uptake.
This illustrates how technology adoption often follows an S-curve, highlighting the critical factors contributing to the inflection point.
- Manufacturing Production: A company ramping up production for a new product line might experience an S-curve pattern. The data sources for this analysis would include production output data, material procurement data, and labor hour statistics. Analysis reveals how initial difficulties in scaling production, like equipment setup or workforce training, create a slower start. The S-curve model can be used to identify bottlenecks and adjust strategies to accelerate production growth and optimize the use of resources.
- Market Penetration of a New Drug: A new drug’s market penetration might follow an S-curve pattern. Data sources would include sales figures, regulatory approvals, and clinical trial results. Analysis would show the drug’s gradual adoption, accelerating once it gains approval and positive clinical feedback. The S-curve analysis can aid in understanding the time it takes for the drug to reach maximum market penetration and what factors might affect this.
Data Sources for S-Curve Analysis
The data utilized for S-curve modeling is crucial for the accuracy of the results. The specific data needed will depend on the specific application, but common data types include:
- Sales figures: Monthly or quarterly sales data provide insights into market penetration and growth.
- Production output: Track the rate at which products are being manufactured over time. This data is important for identifying scaling limitations and bottlenecks.
- Market share: The percentage of the total market that a company controls, or a product occupies, provides insights into relative growth.
- Customer adoption rates: Data on the number of customers adopting a new product or service, gathered over time, provides insights into the rate of uptake.
- Financial reports: Company financial data can reflect revenue and growth patterns over time.
Step-by-Step Guide: Applying S-Curve Method to a Dataset
This guide Artikels a general approach for implementing the S-curve method to a dataset, using sales data as an example.
- Data Collection and Preparation: Gather relevant sales data over time (e.g., monthly sales figures). Clean and prepare the data by handling missing values or outliers.
- Visual Representation: Plot the sales data against time. Visualizing the data in this way allows for a quick assessment of the overall trend and potential S-curve pattern.
- Model Selection: Choose a suitable S-curve model based on the visual inspection and the characteristics of the dataset. Various mathematical functions can be used, such as logistic or Gompertz functions. The chosen function should best fit the observed trend.
- Parameter Estimation: Use statistical methods or software to estimate the parameters of the chosen S-curve model. These parameters determine the shape and position of the curve.
- Interpretation of Results: Analyze the fitted S-curve. Identify inflection points, saturation points, and growth rates. This analysis provides valuable insights into the trajectory of sales and potential future outcomes.
Interpreting Insights from the S-Curve
Interpreting insights from an S-curve involves understanding the factors contributing to the curve’s shape.
- Inflection Point: The inflection point indicates the point of maximum growth rate. This is a crucial point for strategizing marketing and production efforts.
- Saturation Point: The saturation point represents the limit of growth for the product or service. Analyzing the factors behind the saturation point can lead to new opportunities or strategic pivots.
- Growth Rate: The rate of growth can be analyzed to determine if the current strategy is effective or if adjustments are needed to maintain momentum.
Final Summary
In conclusion, this comprehensive guide to creating S-curve patterns in Microsoft Excel empowers you to analyze data effectively and extract valuable insights. We’ve covered the entire process, from initial data preparation to final visualization. Whether you’re a project manager, sales analyst, or researcher, understanding S-curves can significantly enhance your ability to forecast trends, identify critical points, and make data-driven decisions.
The practical examples and step-by-step instructions will make this a truly actionable guide.